Dense Hofield Network: What is this exactly?

Dense Hofield Models

Inspired by the paper Hopfield Networks is All You Need by Ramsauer et al. (2020), I have been experimenting with dense hopfield networks and found a (probably not) novel way of stacking, randomly initialized, hopfield networks and training them via SGD and MSE loss to have the output of the last hopfield layer matched to mnist digits. This achives beautiful representations inside the hofield “image database”.

My Intuition for Dense Hopfield Networks

Dense hopfield networks only use two mathematical operations: matmul and softmax that is it! The following graphic explains it best:

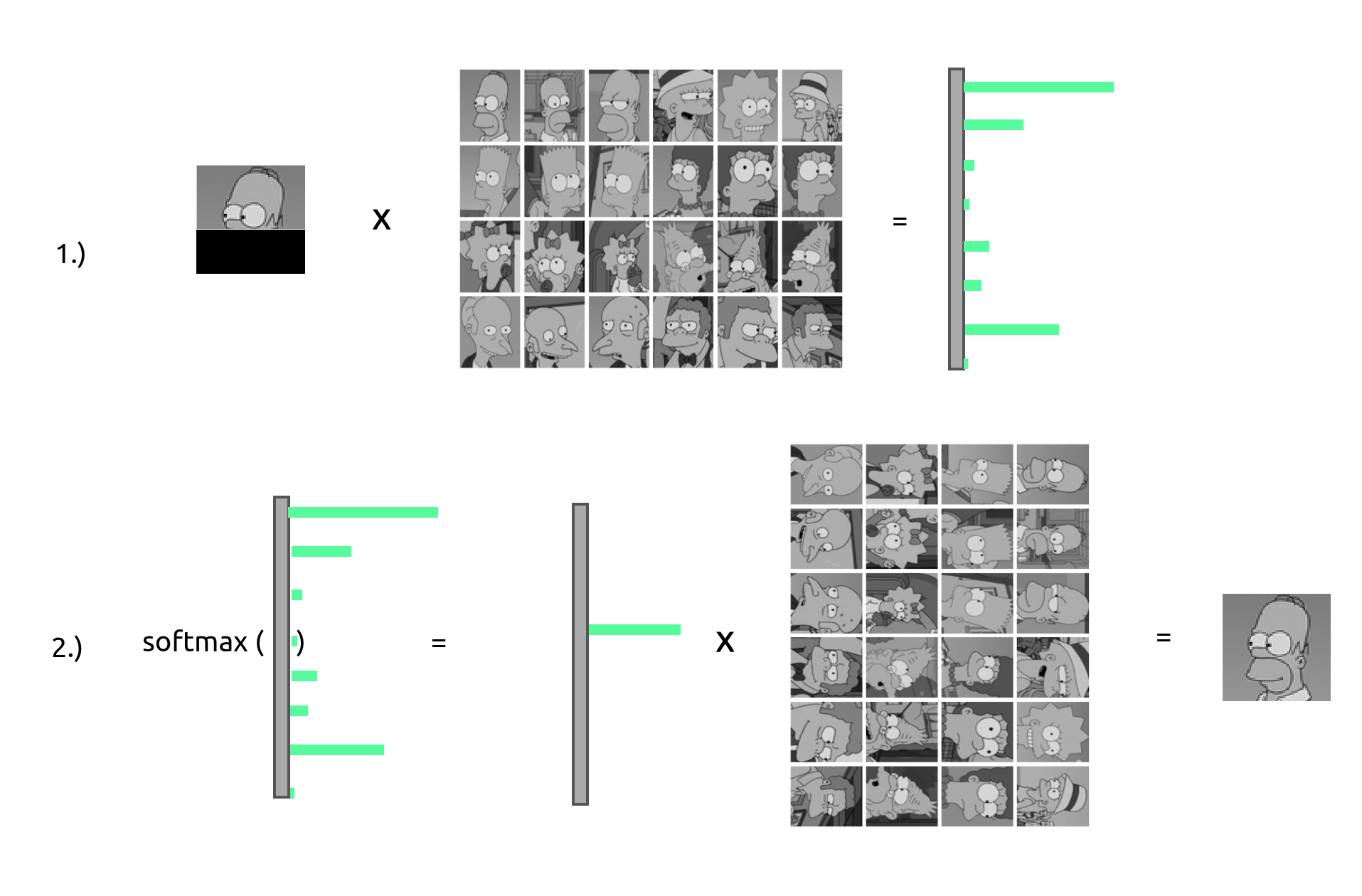
Taken from https://ml-jku.github.io/hopfield-layers/ and edited by me.

A simple intuition for dense hopfield networks: They are like an “image database” H where for a given input image I, we first multiply the transpose of the input with the hopfield database matrix I.T*H. This yields a new vector C = I.T*H that holds the “correspondence” of the input image I to every image in H. Now we apply the softmax function on our “correspondence” vector C. This yields P = softmax(C), lets call it the “probability vector”. With an untempered softmax function, we expect a singular value to be weighted with almost 100% of the probability assigned to it. (Later I will introduce temperature, a tempered softmax function for better representation entanglement and loss signal).

To retrieve the result image R from H the hopfield “image database”, we simply multiply the transposed, softmaxed “probability vector” P with the hopfield database matrix H and we get R = P.T*H where R is the retrieved image from the database H.

Clarifications and infos for implementaiton (mnist example)

Mnist image dimensions = 28px * 28px
flattened = 784px
lets say our hopfield database has 10 images in it then H is a 2d tensor with shape:

H.shape = (10, 784)
I.shape = (1, 784)
C.shape = (1, 10)
P.shape = (1, 10)
R.shape = (1, 784)

Here an example where we fill the hopfield database H with sequences of numbers from 0 to 9 and we start with a different offset on every row. The target sequence we are looking for is [4,5,6,7,8,9,0,1,2,3] but some indicies (values 5 and 1 are) are zeroed out -> [4,0,6,7,8,9,0,0,2,3]. We want to retrieve the target [4,5,6,7,8,9,0,1,2,3] sequence from the database H.

We now softmax the correspondence vector C: [188, 228, 268, 218, 178] becomes [0, 0, 1, 0, 0]

At the end we get [4,5,6,7,8,9,0,1,2,3] just like we wanted 🎉.

TODO

more is coming